Temple Of Man Design Criteria
The major work of Schwaller
de Lubicz in his two huge volume books “The Temple of Man” and the
contributions of his step-daughter Lucie Lamy are finally given their proper
respect in the academic community via some modern technical analysis. A composite diagram from those books was
imported into ACAD AutoSketch and precision ACAD lines constructed over the
original scan. There is nothing magic or super high tech about this
approach. The solution of 8 separate
equations is just a more complex extension of high school mathematics. The use of MathCAD from Mathsoft makes it all
seem simple for those mathematically challenged.
In the CAD system lines are
drawn very precise and thin to fit the image as close as possible. The lines in the image are made large to be
more visible. It is amazing how the dimensionless ratios match up to five
digits of precision. On the left side,
note that in each rectangular area “angle A”
is at eleven o’clock and “B”, “C”
and “D” follow clockwise. This
diagram is repeated below for ease of reference.
One can see two separate ratios develop the same product in the diagram below.
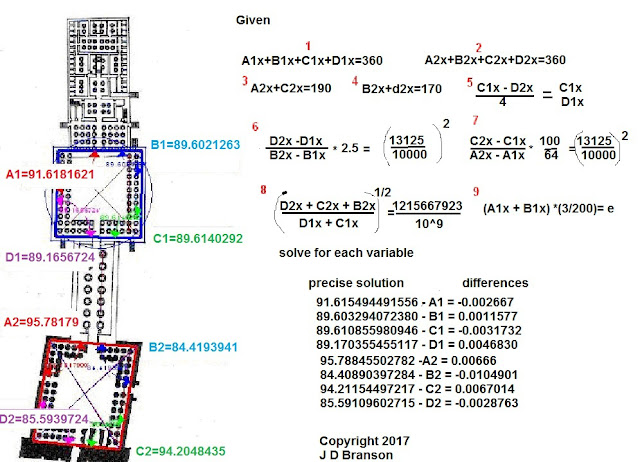
The setup for the Mathcad model is shown below and
developed from the relationships in the diagram above. The number (13125/10000)^(2) = 1.722656 suggested
by 1.7228118.
Obviously the second column
is the one appropriate for the design. If one simply redrew outline around the
two areas, all the angles would change a very small amount, but the ratios
would remain about the same. One cannot
fudge one angle without at least one other angle changing with it. The only way
the given rectangle of angles can improve is by substituting the angles from
the model.
It should be obvious that
this so-called Temple at Luxor was not built to be a work of art or a magical
place to sacrifice virgin goats. You can
see the ACAD measured angles are given in the top blue rectangle as A1, B1, C1 and D1
clockwise and color coded. Corresponding angles for the lower rectangle are
shown in the red box with the same color coding clockwise.
One might be intrigued by how
the Temple Designer decided to select these particular angles, since they vary
from 90 degrees sufficiently to suggest they were not trying to be right angles
and the simple difference from 90 indicate no obvious pattern. With 8
individual pieces of data, there are a very large number of potential
combinations for which there might be some clue as to why this particular
distribution of angles was selected. (see www.giza-footprint.blogspot.com
) For a similar differentiation from perfect right angles.
Model repeated for ease of
use:
In the nine identities shown
in black (numbered in red), the first two are obvious in that the sum of the
angles of any rectangle must be 360 degrees. The second two were easy to find
in a spreadsheet by just checking the sum of various pairs. It is not so much that these two sums were
nice round numbers like 190 and 170, but that all the rest were nothing even close
to any type of system in the sums.
In the 5th identity,
it was natural to check the difference of two angles and also to check
dimensionless ratios of two angles and since the answer to each was similar
there was no separate identity to set them to, so they were just set equal to
each other. At this point one does not even suspect that there will ever be
enough identities to even think about a solution. But we know the
designer/builder put a lot of effort into the Temple, and surely he had some
reason for picking the angles.
Identities 6 and 7 begin to
take the analysis into a whole next level of analytical curiosity. The
differences are all angles from the same orientation but different
rectangles. So the letters are all the
same (D2 and D1) and the subscripts in the same orientation (smaller blue
rectangle angles subtracted from the larger red rectangle angles). There are
potential for negative differences but a ratio of two negatives such as
identity 6 is still a positive ratio.
One might question why
13125/10000? From other work such as the
analysis of basic hydrogen wavelengths in the Lyman Series, the ratio of the
most abundant hydrogen wavelength to the smallest listed one of that group is
1.3125, suggesting that 1.3125 has some fundamental use within hydrogen
structure. The use of the number without
decimals tells MathCAD that this is a precise number and not a four point
decimal of modest precision. At this
point, one has no clue that there is anything important about these identities
and they are simply included in a trial operation to determine if they have
some contribution towards the angle selection process of the Temple Layout
angles.
The number 8 identity follows
this same thinking in that the wavelength of the hydrogen most abundant isotope
is typically given as 1215.668 angstrom. If the original ACAD data had not
given this as 1.2156XX, it probably would have been discarded as an accident. From other work, there is reason to suggest
1215667923 as a more precise value for this wavelength, but in fact the number
1215668000 provides a very similar symbolic result. In the system solution, this identity must
have some unforeseen flexibility. This feature is typically not possible with
most simultaneous equation solutions.
The ninth identity was a
total shock and little hope was taken that it might in fact work with the
others in some type of precise symbolic solution. But the data said it was potentially there,
so why not try it before looking for something else.
Now there are 9 identities
and only 8 variables, so there is reason to believe that there might be some
potential solution. Typically in such
matters, one does not find a precise solution but can maybe find a minimum
error result which might still indicate that the overall design criteria used
something similar. It was a total shock
that a symbolic result popped up whereby all identities are confirmed to in
excess of 14 digits. Typically in
algebraic problems we use to teach the solving of simultaneous equations, we
use very simple and easily graphically plotted equations like 4x – y = 3. Even in industrial problem solving such as
chemical reactors, there seldom is anything of this level of complexity and
never, to my knowledge, involves basic hydrogen structure and the irrational
number, natural log base e = 2.71828.
The actual symbolic solution
shown below is a complex set of equations for each angle variable. Note as in the analysis of the Great Pyramid
footprint that one angle d1x is the basis
for all the others. It is amazing below how many of the same numbers with the
same decimals repeat as much as they do.
Considering the very
fastidious nature of the Lubicz family including the step-daughter Lucie Lamy,
one might conclude that measurements maybe were taken to something like a
millimeter similar to the Cole Survey on the Great Pyramid. In drawing the measurements onto a large
piece of drawing paper, Ms Lamy might have attained accuracies of a small
fraction of a degree. But with the use of ratios, sometimes apparent accuracies
are improved by the cancelation of errors in both the numerator and
denominator.
Since the author is an
engineering manager and programmer, the reader might be tempted to suggest that
the angles measured in ACAD were shifted to enhance the precision of the
measured data. But please examine the
identities and try to conclude which way one might shift the data to even make
it come out closer. You are absolutely
constrained by the sums to always be 360 degrees. The sum to 190 and 170 leaves you with no
idea which way to go with either one. As
it turns out, the number 3 and 4 identities are redundant and either one can be
left out with the same solution, thereby making 8 variables and 8 equations.
If one were using the minimum
error approach, one could shift variables one at a time in an attempt to
minimize the overall error, but with industrial problems this seldom leads to a
symbolic solution if one is not eminent anyway.
And 8 variables is a lot of trial and error approaches which would take
perhaps many man-months of activities. In a looping program, 8 variables taken
to a precision of just 4 digits (10,000 to the 8th power) might take
months or more for a large computer to process.
But the reader needs to keep
in mind that even if a very skilled programmer was able to make adjustments to
the minimum error and ultimately find the symbolic solution, it does not change
the fact that the solution does exist and fits the best measureable data to a
supremely precise fashion. Can anyone provide a better explanation for the
design criteria of the major rectangular areas? The probability of this precise
model fitting randomly created angles is something like one in trillions of
trillions.
What Does the Model Say?
If we were to walk thru the
Temple, we cannot even see the entire layout in our vision. We would have no idea whether some areas are
perfect squares, rectangles or even curved slightly. Therefore, the purpose of
the design layout cannot be to impress a casual observer with a precise
artistic vision. No doubt anyone would
be impressed with the large structure, but little else is casually noticeable.
But why do modern tourists walk thru the Temple and repeatedly come away with a
feeling of something much greater?
Where identities 3, 4 and 9
have only two variables, one can easily plot lines by substituting a value X for
one and plotting the other at Y. This
produces three parallel lines all fairly close to each other because all values
are between say 83 and 96 degrees for X or Y. We can likewise, plot for
identities 6 and 7 the differences for the numerator and denominator. We again find lines parallel to the
identities 3, 4 and 9. When we complete
all that can be done graphically with these five identities, we find a series
of parallel lines all at a slope of 1 to 1.
This greatly improves the probability that a solution might exist. It also proves that there was some design
intent and these are not just random angles
Of course, with computer
software such as MathCAD we can simply throw everything into the solver and it
either finds something or it doesn’t. In
a matter of a few minutes, several strategies can be tested. In this case,
something was found from the very first try.
There were absolutely no adjustments made from the initial readings in
ACAD.
What might the model be
trying to signal to someone that is trying to understand the angle selection
process?
The use of 1.3125 could
simply be a coincidence, since the ratio is repeated in nature regularly. But
the use of 1.215668 is a very unlikely number to occur without the user knowing
something about hydrogen fundamentals. The use of natural log base “e” suggests
a higher understanding of mathematics than we typical ascribe to the ancients,
although the sums of fractions was long in use and that parallels the use of
logarithms. But the fact that five identities were plotted at the same 1 to 1 slope
in the same direction indicates to me that the design had some superior
mathematical capabilities, perhaps in excess of our typical modern
capabilities. In modern teaching of simultaneous equations, it would take the
professor far too long to come up with complex examples that worked using 8
variables, so the tendency in instructional problems is to use three or four
simple ones even when using Matrix manipulations.
It is likely that thousands
of people have scratched their heads trying to figure why the Temple was built
the way it was. Since Google Earth came along, we have had a much better chance
of viewing the entire structure at one time. The problem with dimensions is
that most are unsure what units of measure to use. My approach has been to mostly use only
dimensionless ratios of lengths, areas and perimeters. Angles have been used at 360 degrees for
circles for a very long time and so are much more reliable.
This analysis is just on the
angles. Look at how much more there is
to analyze. From work done on acoustic resonator chambers, the main temple area
looks to be some type of acoustic coupling between say vibrations in the ground
and the Schumann Resonance in the atmosphere initiated by lightning around the
world.
What the Temple of Man
actually did is still to be discovered. But certainly it indicates an
understanding of mathematics and fundamental knowledge heretofore thought
unattainable by early mankind. And without any doubt, if we were to construct
something similar in modern times using perfect rectangles or squares, there
would be absolutely no analysis even possible, as the layout would be as dumb
as the objects are these days using our “modern methods” of designing for
minimum strength and optimization of materials used..
Identities 5, 6, 7, and 8
have three to five variables and are impossible to use in some simple graphic
format. One would have no idea what to do with any single variable, let alone a
group of four or five.
The only way to fully appreciate the design is thru precise measurements
and drawings as provided by Lucie Lamy.
And that information needs to be taken to the next higher level via
modern technology to fully appreciate the message and perhaps functional
purpose of the Temple. We must simply allow ourselves to think
outside of the perpetually
blind box that the designers had no technologies.
This simple graphic below demonstrates
that the Temple of Man is indeed a masterful design and likely does much more
than mankind has even thought about up until this time. Other technical
analysis indicates that this Temple is an acoustical engineer’s delight if we
could get more technical people interested.
It would seem that everybody
could see that the construction was done with purpose. It just is not obvious what the design intent
was. However, in Google Earth it is easy to determine that the offset angle
below is very precisely similar to the Giza Pyramid angle which in turn is
similar to the stars in Orion Belt. However, if instead using the lower star,
one points to the Horsehead Nebula, the angle is exact. It could be that the Orion Belt is used to
attract attention to that general location and then refine the search to the
Horsehead Nebula where there could be many planets and advanced intelligent
life.
It does not seem likely that
the layout of the Temple of Man and the Giza Pyramids is all some type of
accident with construction folks drinking too much beer. It seems obvious the
two designs are very similar in overall layout. If the design was in fact
created by advanced civilizations for somewhere in the area of the Orion Belt,
wouldn’t it be smart to study it a bit more and see if we could learn something
useful.
Copyright 2017 All Rights
Reserved J. D. Branson
bransonjim9 at gmail dot com
Check out other blogs on my
profile





No comments:
Post a Comment